This post discusses the risk parity framework and maximum diversification portfolio. Then backtest the monthly portfolio rebalance strategy across five portfolios: minimum-variance, maximum-Sharpe, most-diversified, risk-parity, and equal-weights.
Introduction
In previous post we reviewed the basics of mean-variance optimization (MVO), and portfolios such as minimum variance and maximmum sharpe. This post continues to discuss some popular practices in asset allocation, namely risk parity and maximum diversification. Then we evaluate these allocation strategies using historical market data.
It is known that all these portfolios are special cases of MVO under some conditions. For example, MVO becomes minimum variance if expected reutrns are equal; it coincides with maximum diversification if return-risk ratios are the same across assets ([2]). The portfolio selection depends on our information and knowledge about the market. If expected return and risks are known with certainty, a maximum sharpe ratio is good choice. If expected return is hard to measure, covariance knowledge can be leveraged to construct minimum variance or risk parity portfolios. If we have no knowledge at all about the market, a naive equal-weighting portfolio will be a default option, which is also served as benchmark in our backtest.
Risk Parity and Maximum Diversification
Risk parity was coined by Edward Qian ([1]) and popularized by Bridgewater all weather fund. It focuses on budgeting and allocation of risks rather than capitals. The essence is equal/parity risk contribution (ERC) defined as
\[ \begin{aligned} MRC_i&=\frac{\partial \sigma_p}{\partial w_i}=\frac{\sum_{j=1}^nw_j\sigma_i\sigma_j}{\sigma_p}=\frac{(\Sigma w)_i}{\sigma_p}\\ RC_i&=w_i * MRC_i \end{aligned} \]
Note that ERC weights are not necessarily proportional to inverse volatililty. In fact, [3] gives the solution as to minimize
\[ f(x)=\sum_{i=1}^{n}\sum_{j=1}^{n}\left( w_i (\Sigma \cdot w)_i - w_j(\Sigma \cdot w)_j\right)^2 \]
Risk parity is embedded with momemtum features that may cause a problem when its followers stampede in the market. If stock market suddenly collapses, stock's risk will spike which in turn demands less asset allocation on it. The liquidation will then reinforce the sell-off.
Maximum diversification portfolio tries to maximize the ratio of weighted average volatility over portfolio volatility as \[ \underset{w}{\max} \frac{w^T \sigma}{\sqrt{w^T\Sigma w}} \]
which can also be solved numerically.
Assessments
Let's compare long-only portfolios consist of five stocks, SPY, EFA, TIP, GSG, and VNQ, to represent US, international, treasury, commodity, real estates, respectively, between 2011-2019. The portfolios include minimum variance, maximum sharpe, risk parity, and maximum diversification, rebalanced at month end. Benchmark is equal-weights. The code can be found on Github.
First of all, results below show none of them have CAGR above equal weights. It may well be due to the hostorical long bull market after 2008-2009 financial crisis. GMV has the lowest risk, which is expected, and the highest Sharpe ratio. The maximum diversified portfolio has the second lowest volatility, and second highest Sharpe. Controlling risk is a feasible way to achieve high Sharpe, but may comes with the cost of low returns, especially in bull markets. Equal weights has the biggest drawdown among the five, dragged by commodity underperformance, but then fully recovered. Risk parity follows closely maximum diversified in the beginning, and then outperform marginally in Elliott wave 3 and 5.
1 | gmv sharpe diversified risk_parity equal_weights |
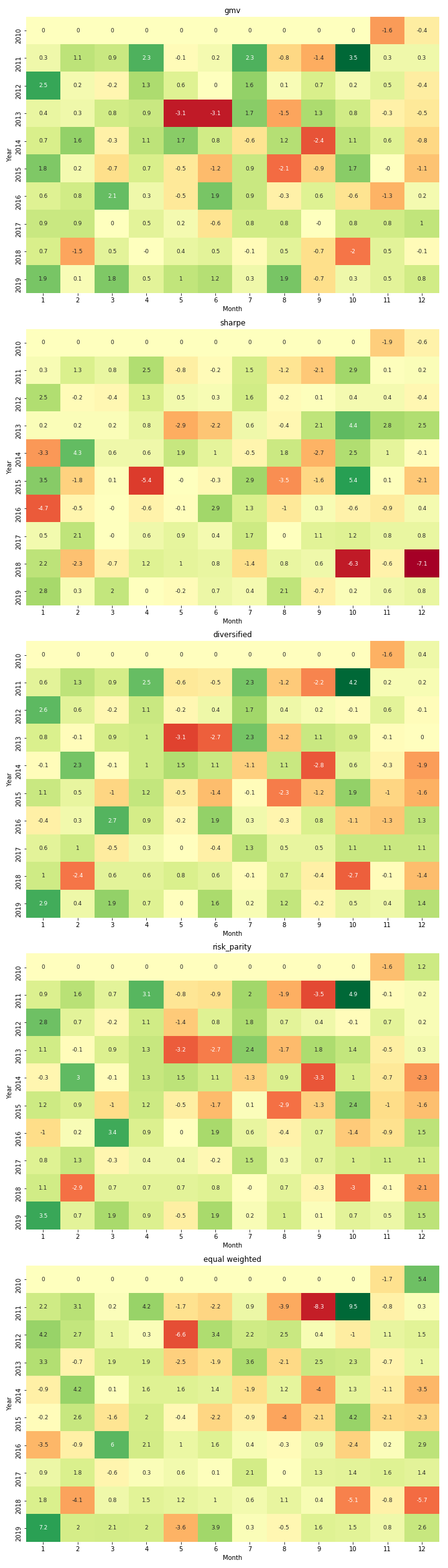
The portfolo values over time and monthly returns are shown as blows. During this period, domestic stocks went up the most, followed by real estates. Commodities is the only one that went south. GMV essentially dodged the market pull back at the end of 2018, yet it also missed the market recovery afterwards.
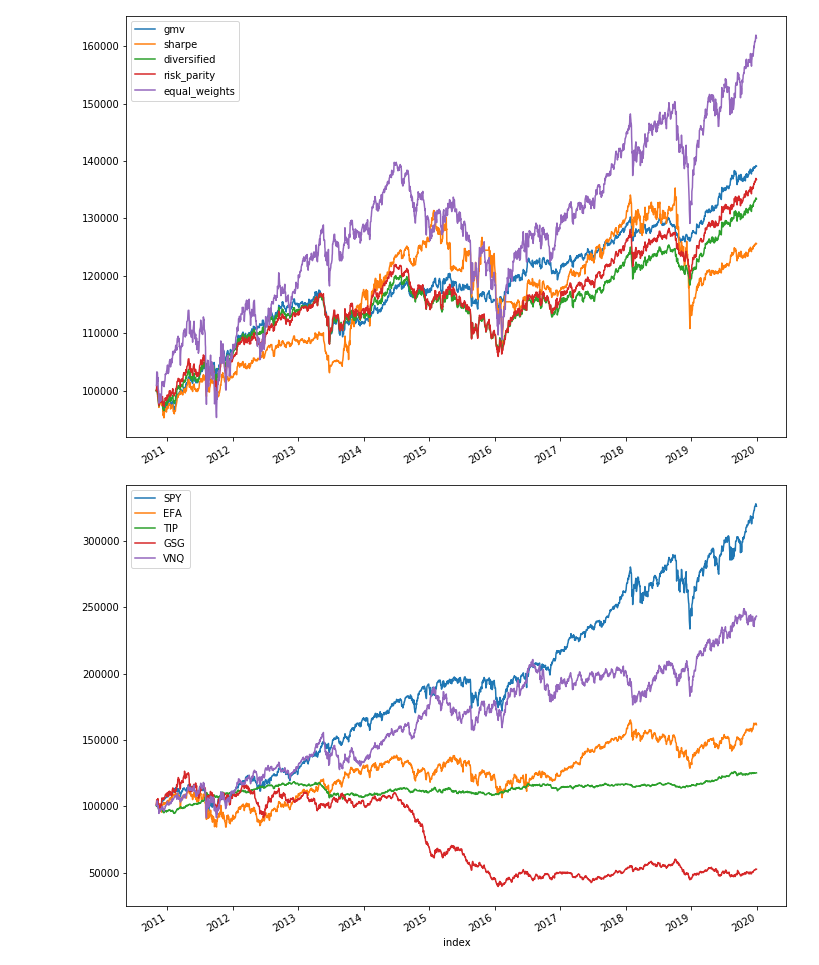
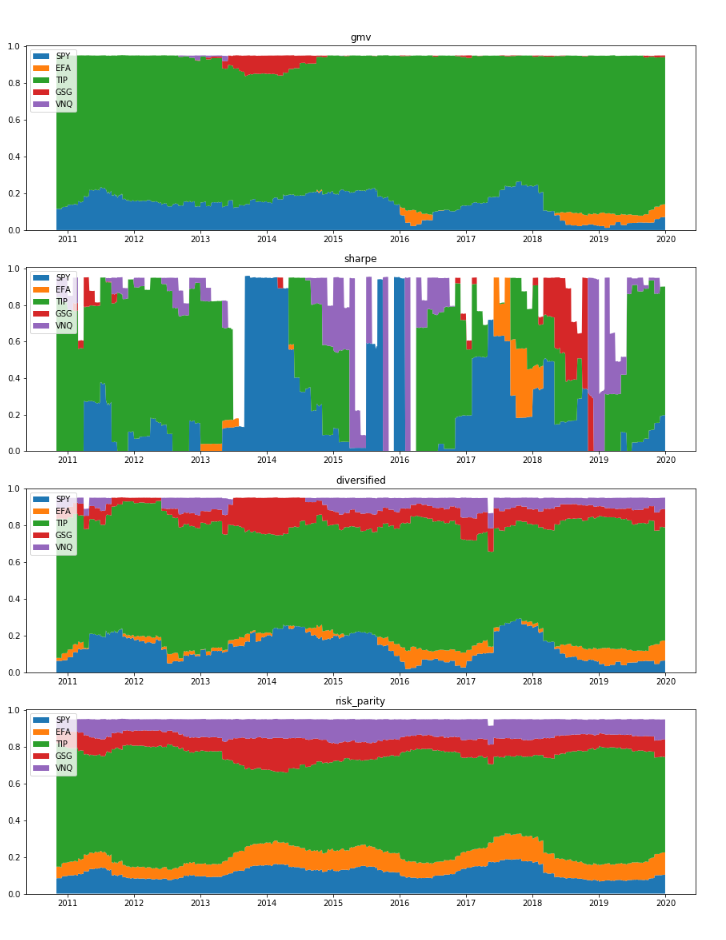
The stock holdings below explains why they are all behind equal weights, because they hold too much Treasuries in the bull markets. GMV has predominantly treasuries and S&P500. The maxinum sharpe portfolio is somehow agressive and unstable. It has the biggest rotation costs, and sometimes it holds all stocks, sometimes it holds all cash.
Reference
- Qian, Edward. "Risk parity portfolios: Efficient portfolios through true diversification." Panagora Asset Management (2005).
- Roncalli, Thierry. Introduction to risk parity and budgeting. CRC Press, 2013.
- Maillard, Sébastien, Thierry Roncalli, and Jérôme Teïletche. "The properties of equally weighted risk contribution portfolios." The Journal of Portfolio Management 36.4 (2010): 60-70.
- Spinu, Florin. "An algorithm for computing risk parity weights." Available at SSRN 2297383 (2013).
- Bender, Jennifer, Thomas Blackburn, and Xiaole Sun. "Clash of the Titans: Factor Portfolios versus Alternative Weighting Schemes." The Journal of Portfolio Management 45.3 (2019): 38-49.
- The Quant MBA
DISCLAIMER: This post is for the purpose of research and backtest only. The author doesn't promise any future profits and doesn't take responsibility for any trading losses.